Lab 12 — Animating Grids
In this lab you will animate a two-dimensional grid. The lab doesn’t actually require much new from you — just more of the same things you already know about grids and functions. We have done all the drawing and animation for you.
Download the lab 12 files to get started.
❤️ Take heart! This lab looks long but that’s just because we’re being very thorough explaining everything. There are just five functions to write and we have provided you all the documentations and tests. Once you get the functions written for a problem, you’ll be able to have a lot of fun playing with the animations.
Waterfall
In this problem, water appears at the top of the grid, then moves downward,
avoiding rocks along the way. Every cell in the grid is either a rock 'r',
water 'w', or empty None. Every round, every water moves downward if
possible or disappears if there is no possible move.
Is a move OK?
First, write the function called is_move_ok(grid, x, y). This function takes
three parameters:
grid: a grid with some rocks and some waterx: x coordinate to checky: y coordinate to check
This function returns True if the coordinates (x, y) are valid and that cell
is empty. Otherwise it returns False.
You can think of this as three rules:
-
Check if
(x, y)is in bounds, and if it is not, return False. -
Check if
(x, y)is empty, and if it is not, return False. -
Otherwise (by default), return true.
We have provided doctests for you — be sure you can pass these before you move on.
Move water
Now write the function called move_water(grid, x, y). This function takes
three parameters:
grid: a grid with some rocks and some waterx: x coordinate of some watery: y coordinate of some water
This function assumes that the coordinate (x, y) contains water. It then moves
this water downward if possible, following these rules:
-
Move down first if possible. If the square directly below the water is a valid move, move the water there and take no further actions.
-
Move down-left if possible. If the square down and left is a valid move, move the water there and take no further actions.
-
Move down-right if possible. If the square down and right is a valid move, move the water there and take no further actions.
-
Water is blocked. If the above three moves are all invalid, the water disappears from the world.
Be sure to take only one of these actions.
We have again provided doctests for you.
Running the program
You can run this program from the command line as follows:
python waterfall.pyThe program accepts the following arguments:
--width: width of the board, 30 by default--height: height of the board, 30 by default--speed: speed of each round, 500ms by default--scale: scale of board, 10 by default--water-factor: amount of water on board, given by 1 out of this water-factor, which is 20 by default--rock-factor: amount of rock on board, 1 out of this rock-factor, which is 10 by default
For example:
python waterfall.py --width 50 --height 50 --water-factor 10 --rock-factor 4This will run the waterfall program with a width of 50 and a height of 50, with 1/10 of the cells at the top generating water and 1/4 of the cells initialized to have rocks.
The rest of the code
Move all water
This function moves all the water in the grid down one space if possible
(otherwise that water disappears). We just need to loop through all the grid
cells and call the move_water() function you wrote if that cell has water.
One trick we use is to cover the rows from the bottom up. This avoids us moving
a cell with water more than once. The function called reversed takes the list
of numbers generated by range() and reverses them, so we count from the
maximum value (minus 1) down to zero.
def move_all_water(grid):
"""
Move all of the water down once (for one round).
:param grid: a grid with rocks and water
:return: the modified grid
"""
# tricky: do y in reverse direction (from the bottom up), so each
# water moves only once.
for y in reversed(range(grid.height)):
for x in range(grid.width):
if grid.get(x, y) == 'w':
move_water(grid, x, y)
return gridCreate water
This function creates water along the top of the grid. It uses a parameter
called water_factor to control the probability with which water is created.
The probability is 1 / water_factor, so if water_factor is 10, the probability
is 1/10.
def create_water(grid, water_factor):
"""
Create water at the top of the grid. Create water at the top of the grid. The probability of creating water for any cell is 1 / water_factor.
:param grid: a grid with rocks and water
:param water_factor: a factor controlling how often water is created
:return: the modified grid
"""
for x in range(grid.width):
if random.randrange(water_factor) == 0:
grid.set(x, 0, 'w')
return gridCreate rocks
This function creates rocks in the grid at the start of the program. It uses a parameter called `rock-factor to control the probability with which rocks are created, similar to the water.
def init_rocks(grid, rock_factor):
"""
Initialize the grid with rocks. The probability of any cell containing
rock is 1 / rock_factor.
:param grid: an empty grid
:param rock_factor: a factor controlling how often rocks are created
:return: the modified grid
"""
for y in range(grid.height):
for x in range(grid.width):
if random.randrange(rock_factor) == 0:
grid.set(x, y, 'r')
return gridDo one round
This function does one round of the animation. It creates water at the top, draws the grid, and then moves all the water.
def do_one_round(grid, canvas, water_factor, scale):
"""Do one round of the move, call in timer."""
create_water(grid, water_factor)
draw_grid_canvas(grid, canvas, scale)
move_all_water(grid)Conway’s Game of Life
Conway’s Game of Life was developed in 1970 by British mathematician John Horton Conway. The game is perfectly suited for a Grid because it uses a two-dimensional grid of cells.
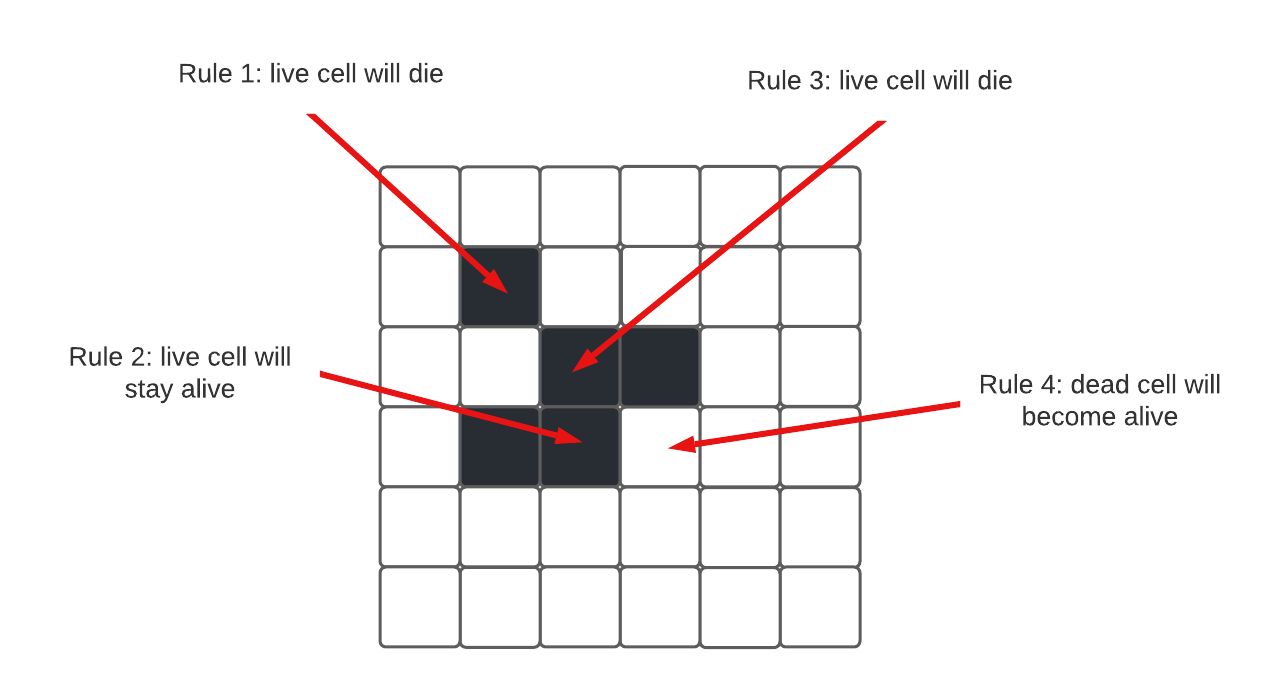
The rules of the game try to mimic how life is created. Every cell in the grid represents a living organism if it is filled in as a black rectangle. Otherwise the cell is dead and shown as white. The game consists of a series of rounds. During each round, each cell can either become alive, can die, or can stay the same. The “survival” of each cell in the next round depends on its neighbors:
- underpopulation: any live cell with fewer than two live neighbors dies
- suitability: any live cell with two or three live neighbors lives on to the next generation
- overpopulation: any live cell with more than three live neighbors dies
- reproduction: any dead cell with exactly three live neighbors becomes a live cell
Using just these simple rules, and an initial starting condition, complex interactions can occur. For example, this pattern, called a block-laying switch engine, has infinite growth and leaves behind small squares.

We will build the entire Conway’s Game of Life with suprisingly little code. The game consists of five files:
-
life.py— contains the main program, methods for creating a grid, and the logic for manipulating the grid according to the rules of the game -
conway_starters.py— contains some sample ways to initialize the game -
lifeutils.py— contains some simple utilities for the game -
drawcanvas.py— contains methoids for drawing on a rectangular canvas -
utilities.py— some helpful functions for animating the game
Reminder: All the code you will write is in life.py.
Helpful Utilities
Before we get to writing code, here are some helpful functions you can use.
These are all written for you in lifeutils.py:
-
make_alive(grid, x, y): Make a cell be alive (represented as a black rectangle) -
make_dead(grid, x, y): Make a cell eb dead (represented as a white rectangle) -
is_alive(grid, x, y): Returns True if the cell is in bounds and alive, otherwise False. -
is_dead(grid, x, y): Returns True if the cell is in bounds and dead, otherwise False. -
wrap_x(grid, x): Checks if anxvalue is off the grid and if so, wraps it around to the other side. -
wrap_y(grid, y): Checks if ayvalue is off the grid and if so, wraps it around to the other side.
These last two functions are particularly helpful because Conway’s Game of Life is designed for an infinite grid, but we will be playing a finite grid. To get most of the benefits of the game, we can wrap around the grid at the edges. We’ll explain this more below.
Random Placement
Write a function that will randomly initialize the grid with alive squares.
Write your code in random_placement(grid). We have provided documentation and
doctests for you.
⚠️ Be sure to test your function with doctests and get it working before moving on to the next function.
This function should loop through all of the cells in the grid and populate 20%
of them. You can use random.randrange(10) to get a number between 0 and 9, and
then mark a cell as alive if you get a 0 or 1. Use the make_alive() function.
Notice that the doctest for this function uses random.seed() to test the
function deterministically, like we discussed in lecture.
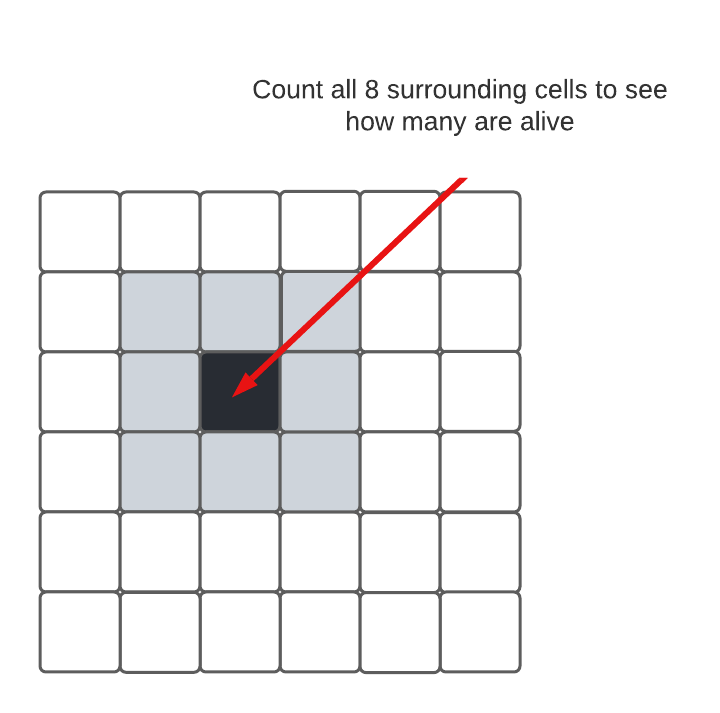
Count Alive Neighbors
Write a function that counts the number of alive neighbors a cell has. Write
your code in count_alive_neighbors(grid, x, y). We have provided documentation
and doctests for you.
⚠️ Be sure to test your function with doctests and get it working before moving on to the next function.
This function should check all 8 neighbors of the cell at coordinate (x, y) and count how many are alive. Use the accumulator pattern!
Here is an example showing the 8 neighbors that need to be counted to see how many are alive:
Normally, this game is played on an infinite grid. However, we will be using a
finite grid. As a result, we will need to wrap around in both the x and y
directions when counting neighbors. For example:
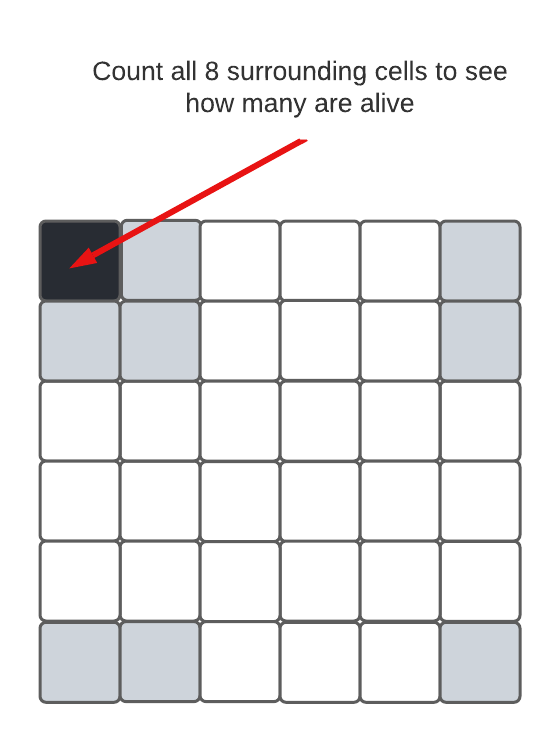
You should use the wrap_x() and wrap_y() functions discussed above. For
example, if you are checking the neighbors of cell (0, 1), you can check the one
above it by using:
y_minus_1 = wrap_y(grid, y - 1)
is_alive(x, y_minus_1)Reminder: Note that you can use these functions in all cases (whether a cell is near the edge or not), and they will do the expected thing when not wrapping. This will make your code simpler — just assume every cell is near the edge and has to deal with wrapping.
Conway Rules
Write a function that modifies the gid based on Conway’s rules for the game.
Write your code in conway_rules(grid). We have provided documentation and
doctests for you.
⚠️ Be sure to test your function with doctests and get it working before moving on to the next section.
This function should loop over all cells in the grid, count the number of alive neighbors each cell has, and then apply Conway’s rules. The rules can be stated more succinctly as:
- Any live cell with two or three live neighbors survives.
- Any dead cell with three live neighbors becomes a live cell.
- All other cells become or stay dead.
You can use make_alive(grid, x, y) to make a cell be live, and
make_dead(grid, x, y) to make a cell be dead.
Reminder: The game is run in rounds. The grid you are passed is for the
current round. You need to create a new grid and set alive/dead cells in this
new grid that represents the next round. The function should return this new
grid.
This makes a lot of sense if you think about it. If you tried to apply the rules to the current grid, then you would be making new cells come alive as you loop through it, causing all your calculations to be off!
You will notice that we have quite a few doctests. Many of these are taken from the patterns shown in the Wikipedia page for Conway’s Game of Life. They fall into several categories:
-
basic tests: The first two tests cover some simple cases. Note the second one is a little odd — with one row, we wrap above and below.
-
stable formations: The block and beehive tests are two stable patterns that never change.
-
oscillators: The blinker and toad tests are two oscillating patterns.
Running the game
Congratulations, if you have written those three functions, everything else is done for you! The rest of the code draws the grid on the canvas and then animates it.
You can run a wide variety of games with the life.py script. A good place to
start is to run the patterns from the
Wikipedia page on Conway’s Game of Life.
Compare your patterns to the ones on Wikipedia to be sure they work correctly:
python life.py --starter block
python life.py --starter beehive
python life.py --starter loaf
python life.py --starter boat
python life.py --starter tub
python life.py --starter blinker
python life.py --starter toad
python life.py --starter beacon
python life.py --starter gliderIf some of these aren’t working, you will want to be sure you are passing all the doctests for each function.
Once you are satisfied with this, then try running the default setup:
python life.pyThis will create a 30 x 30 grid, using your random_placement() function to
select 20% of the squares to be alive. The speed is set to make one transition
every 1/2 of a second.
Finally, you can use the starters available in conway_starters.py by using:
python life.py --starter [starter]The available starters include:
- stable formations
- block
- beehive
- loaf
- boat
- tub
- oscillators
- blinker
- toad
- beacon
- spaceships
- glider
- lightweight_spaceship
- other
- diehard (dies after 130 rounds — a long time considering it starts with just 7 alive)
- engine (will go forever on an infinite canvas, leaving behind blocks)
For example:
python life.py --starter diehardYou can also control a variety of other aspects of the game with command line arguments. This is the full set of arguments:
--width: sets the width of the board (default 30)--height: sets the height of the board (default 30)--starter: sets the starter (default random)--speed: number of ms between rounds (default 500)--scale: scales the size of the squares (default 10)--offset: moves the starter by some offset in both the x and y direction
You can use the following to get a reminder of the possible arguments:
python life.py -hHere are some good combinations to try:
## good view of the glider
python life.py --starter glider --scale 6 --width 100 --height 100 --speed 3
## slow spaceship
python life.py --starter lightweight_spaceship --offset 10 --speed 100
# fast spaceship
python life.py --starter lightweight_spaceship --offset 10 --speed 3
## fast engine (because the board is small) but stops (because the board is finite)
python life.py --starter engine --speed 10 --scale 10 --width 100 --height 80 --offset 20
## larger, slower engine (because th eboard is big and the scale is small), but goes for longer because there is more room -- can really see its effect
python life.py --scale 4 --width 300 --height 100 --starter engine --speed 30Challenge
This is entirely optional!
You can add any starter you like to conway_starters.py. You will see two
methods of creating them, one with Grid.build() and one with Grid(). You can
find a wide variety of patterns at the
Life Wiki. For example, you might try
initializing this gun. You can launch
the visualization tool and then pause on step 1 to see its initial state.
For some patterns, it might be useful to turn wrapping off. You could write a
version of count_alive_neighbors() that doesn’t wrap. If you wanted a bigger
challenge you could add a command line flag called “—nowrap” that lets you turn
off wrapping on demand.
Some amazing stuff
Lessons
What we want you to get from this lab:
-
You can use a Grid to get and set values
-
You can write functions that operate on grids
-
You are comfortable thinking about problems in two dimensions
-
You can test your functions with doctests
-
You can figure out what went wrong when something unexpected happens
-
Hopefully you had fun!
Points
Turn in a zip file that has your code.
Every function should have a docstring and doctests.
| Problem | Task | Description | Points |
|---|---|---|---|
| waterfall | is_move_ok() | Your solution works | 1 |
| waterfall | move_water() | Your solution works | 2 |
| game of life | random_placement() | Your solution works | 1 |
| game of life | count_alive_neighbors() | All functions have good doctests | 3 |
| game of life | conway_rules() | All functions have good doctests | 3 |