Grids

• when we worked with images, we were manipulating 2-dimensional data
• pixels were in both the X and Y direction

A grid provides generic two-dimensional storage

• you can store strings, integers — anything (just like lists can store anything)

Basic grid commands

• run pip install byugrid before you start using Grid!

from byugrid import Grid

# create a blank grid -- all cells start out with None inside them
grid = Grid(width, height)

grid.width             # grid width
grid.height            # grid height

Basic grid commands

grid.get(x, y)         # gets cell contents at coordinate (x, y)
grid.set(x, y, value)  # sets cell contents at coordinate (x, y) to value
grid.in_bounds(x, y)   # True if the cell coordinates (x, y) are valid

Simple grid example

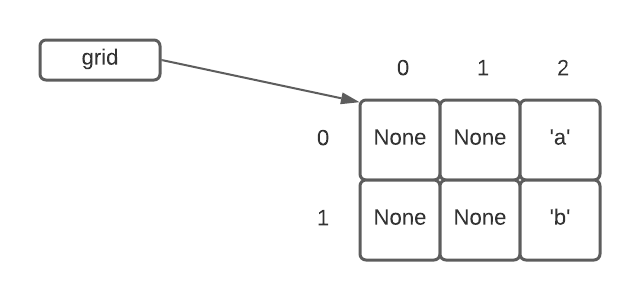
from byugrid import Grid

grid = Grid(3, 2)
print(grid.width)
grid.set(2, 0, 'a')
grid.set(2, 1, 'b')
print(grid.get(2, 0))

    3
    a

Peeps

Peeps in a grid

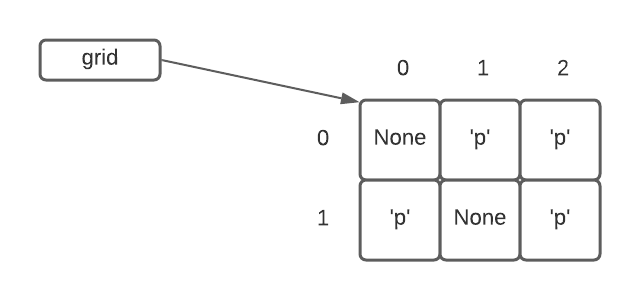
• a square in the grid is either ‘p’ if it contains a peep, or is None if empty

Peeps are happy if another peep is to their left or right

• Is the peep at (0, 0) happy? False -> no peep there
• Is the peep at (1, 0) happy? True -> peep on the right
• Is the peep at (0, 1) happy? False -> no peep on the left (out of bounds) or right (None)

Check if a peep is happy

Step 1: Build the grid

from byugrid import Grid

# Note that we can build a grid with two lists
# Two lists are nested inside of another list -- so a list that has two lists, one for each row
grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])

Step 2: Build is_happy(grid, x, y)

• Given a grid, return True if the peep at position (x, y) is happy, False otherwise
• We will write this in PyCharm, starting with doctests

1. Use the “if/return” strategy — start with the obvious case where there is no peep at (x, y)
2. If we make it past this case, we know we have a peep, so check left and right
   • Be sure to check if the coordinate is in bounds first
   • If either left or right has a peep, can return right away (if we check left first and there is a peep, no need to check right
3. Otherwise, return false

Here is the code we wrote:

def is_happy(grid, x, y):
    """
    Given a grid of peeps and in bounds x,y.
    Return True if there is a peep at that x,y
    and it is happy.
    A peep is happy if there is another peep
    immediately to its left or right.
    >>> grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])
    >>> is_happy(grid, 0, 0)
    False
    >>> is_happy(grid, 1, 0)
    True
    >>> is_happy(grid, 2, 0)
    True
    >>> is_happy(grid, 0, 1)
    False
    >>> is_happy(grid, 2, 1)
    False
    >>> is_happy(grid, 5, 5)
    False
    """
    # your code here
    # check if the grid square is empty
    if not grid.in_bounds(x, y):
        return False
    if grid.get(x, y) is None:
        return False
    # we know we have a peep!
    # check if there is a peep to the right
    if grid.in_bounds(x + 1, y) and grid.get(x + 1, y) == 'p':
        return True
    # check if there is a peep to the left
    if grid.in_bounds(x - 1, y) and grid.get(x - 1, y) == 'p':
        return True
    # all other cases must be false
    return False

An important aspect of this code is the in bounds check:

if grid.in_bounds(x + 1, y) and grid.get(x + 1, y) == 'p':

1. We need to check if a grid cell to the right (or left) is in bounds, because we might be in a cell that is right at the ege of the grid.

2. If we omit this check, we will get an exception that indicates we went out of bounds.

3. By writing the test this way, we first check if (x, y) is in bounds, and if it is NOT, then we never get to calling grid.get. In other words, Python will short-circuit the test of an and and stop if it gets to a False. This avoids having grid.get() cause an exception for points that are not in bounds.

Step 3: Build has_happy(grid, x)

• Given a grid, return True if there is one happy peep in column x
• We will write this in PyCharm, starting with doctests

Here is the code we wrote:

def has_happy(grid, x):
    """
    Given grid of peeps and an in-bounds x.
    Return True if there is a happy peep in
    that column somewhere, or False if there
    is no happy peep.
    >>> grid = Grid.build([[None, 'p', 'p'], ['p', None, 'p']])  # same grid as before
    >>> has_happy(grid, 0)
    False
    >>> has_happy(grid, 1)
    True
    """
    # your code here
    for y in range(grid.height):
        if is_happy(grid, x, y):
            return True
    return False

Step 4: Build has_happy_anywhere(grid)

We had enough time to write this function, which returns true if there is a happy peep anywhere in the grid. This shows how to loop over the grid cells in two dimensions, using nested for loops. We return True as soon as we have found a single happy peep.

def has_happy_anywhere(grid):
    """
    Checks if there is any peep happy anywhere in the grid, True if there is at least one!
    :param grid: a grid
    :return: True if there is at least one happy peep in the grid
    >>> grid = Grid.build([['p', 'p', 'p', None, 'a', 'b'], [None, 'p', None, 'p', None, 'p']])
    >>> has_happy_anywhere(grid)
    True
    >>> grid2 = Grid.build([['p']])
    >>> has_happy_anywhere(grid2)
    False
    >>> grid3 = Grid.build([[None, None, None], [None, None, None], ['p', 'p', None]])
    >>> has_happy_anywhere(grid3)
    True
    """
    for y in range(grid.height):
        for x in range(grid.width):
            if is_happy(grid, x, y):
                return True
    return False

Step 5: Build all_happy(grid)

We had enough time to write this function, which returns true if there all peeps are happy. Instead of checking if all peeps are happy, we return False as soon as we have found a single unhappy peep.

def all_happy(grid):
    """
    Returns true if all peeps are happy
    :param grid:
    :return:
    >>> grid = Grid.build([['p', 'p', 'p', None, 'a', 'b'], [None, 'p', None, 'p', None, 'p']])
    >>> all_happy(grid)
    False
    >>> grid2 = Grid.build([['p']])
    >>> all_happy(grid2)
    False
    >>> grid3 = Grid.build([[None, None, None], [None, None, None], ['p', 'p', None]])
    >>> all_happy(grid3)
    True
    >>> grid4 = Grid.build([[None]])
    >>> all_happy(grid4)
    True
    """
    for y in range(grid.height):
        for x in range(grid.width):
            if grid.get(x, y) == 'p' and not is_happy(grid, x, y):
                return False
    return True